Sistemi di punti materiali
Punto materiale
Il punto materiale è un approssimazione in cui tutta la massa del corpo in studio si concentra in un punto. Questa approssimazione è valida quando le dimensioni del corpo sono trascurabili rispetto alle distanze in questione.
Sistemi di punti
Consideriamo un sistema di $n$ punti materiali, la forza $\vec R_i$ agente sull’i-esimo punto si può esprimere come la risultante delle forze esterne agenti sul punto $\vec R_i^{(E)}$ e delle forze esercitate dagli altri $n-1$ punti, forze interne al sistema, $\vec R_i^{(I)}$:
\[\vec R_i = \vec R_i^{(E)} + \vec R_i^{(I)} =m_i \vec a_i\]Tenendo presente la terza legge di Newton se un punto $i$-esimo esercita una forza $\vec F_{i\rightarrow j}$ su un punto $j$-esimo allora il punto $j$-esimo esercita una forza $\vec F_{j\rightarrow i}$ sul punto $i$-esimo. Tali forze sono uguali in modulo, sono sulla stessa retta d’azione e di verso opposto.
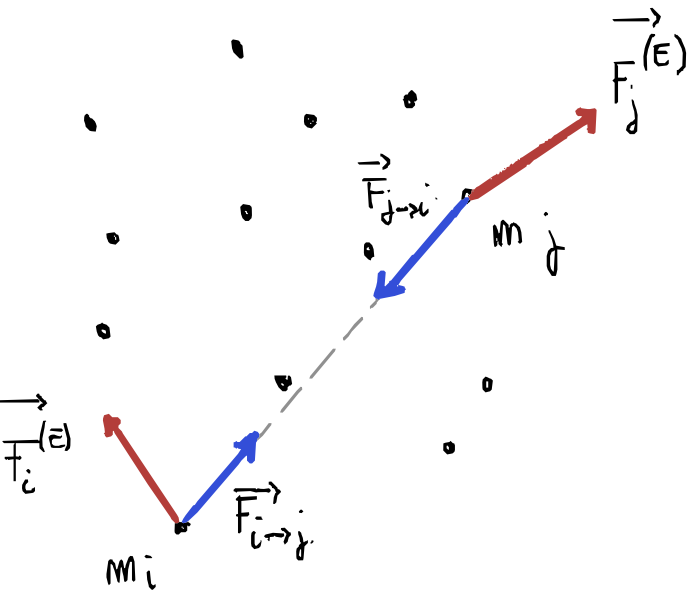
Quindi prendendo in considerazione la risultante nel sistema di tutte le forze:
- esterne
- interne
| $F_{i\rightarrow j}$ | $m_1$ | $m_2$ | $\cdots$ | $m_n$ |
|---|---|---|---|---|
| $m_1$ | $0$ | $F_{1\rightarrow 2}$ | $\cdots$ | $F_{1\rightarrow n}$ |
| $m_2$ | $F_{2\rightarrow 1}$ | $0$ | $\cdots$ | $F_{2\rightarrow n}$ |
| $\cdots$ | $\cdots$ | $\cdots$ | $\cdots$ | $\cdots$ |
| $m_n$ | $F_{n\rightarrow 1}$ | $F_{n\rightarrow 2}$ | $\cdots$ | $0$ |
Il risultato delle forze interne è zero perché in base al principio di azione e reazione esse sono a due a due uguali ed opposte, ne consegue che la risultante delle forze agenti sul sistema:
\[\vec R = \vec R^{(E)}\]Moto del centro di massa
Centro di massa
Si definisce centro di massa di un sistema di punti materiali, il punto geometrico, nel sistema di riferimento considerato, definito dal raggio vettore:
\[\vec r_{CM} = \frac {\sum_{i=1}^n m_i \vec r_i}{\sum _{i=1}^n m_i}\]le cui componenti vanno a definire le coordinate del punto:
\[x_{CM} = \frac {\sum_{i=1}^n m_i x_i}{\sum _{i=1}^n m_i}\] \[y_{CM} = \frac {\sum_{i=1}^n m_i y_i}{\sum _{i=1}^n m_i}\] \[z_{CM} = \frac {\sum_{i=1}^n m_i z_i}{\sum _{i=1}^n m_i}\]Teorema del moto del centro di massa
Esaminiamo $\vec R$:
\[\vec R = \sum_{i=1}^n F_i = \sum_{i=1}^n m_i \vec a_i = \sum_{i=1}^n m_i \;\;\frac {d^2\vec r_i}{dt^2} =\frac {d^2}{dt^2}\bigg(\sum_{i=1}^n m_i \cdot \vec r_i\bigg)\]con $\sum_{i=1}^nm_i = M$ massa del sistema, moltiplichiamo e dividiamo per esso:
\[\vec R = M\frac {d^2}{dt^2}\bigg(\frac {\sum_{i=1}^n m_i \cdot \vec r_i}{M}\bigg)\]con $\frac {\sum_{i=1}^n m_i \cdot \vec r_i}{M} = \vec r_{CM}$:
Questo esprime il teorema del centro di massa:
\[\vec R = M \frac {d^2 \vec r_{CM}}{dt^2} = M \frac {d\vec v_{CM}}{dt} = \frac {d\vec p_{CM}}{dt}\]Il centro di massa si muove come un punto materiale in cui sia concentrata tutta la massa del sistema e a cui sia applicata la risultante delle forze esterne.
In altre parole la risultante delle forze esterne in un sistema di punti materiali è uguale alla massa totale del sistema per la derivata seconda del centro di massa del sistema sul tempo.
O ancora la risultante delle forze esterne è uguale alla derivata rispetto al tempo della quantità di moto totale del sistema
Conservazione momento in un sistema isolato
Un sistema si dice isolato se
- non è soggetto a forze esterne, oppure
- l’azione delle forze esterne è tale che la loro risultante $\vec F^{(E)}$ sia nulla:
Quindi in un sistema isolato la quantità di moto totale del sistema rimane costante nel tempo e il centro di massa si muove di moto rettilineo uniforme o resta in quiete.
Sistema di riferimento del centro di massa
- todo
Domande
1) Terzo principio della dinamica. Se considero un sistema che prevede delle forze di reazione, mi fanno escludere a priori che il sistema sia isolato, oppure non è vero? La legge vale sempre? Quando un sistema si dice isolato?
a) Terzo principio della dinamica
L’enunciato della terza legge di Newton dice:
- se un corpo A esercita una forza $\vec F_{A\rightarrow B}$ su un corpo B allora il corpo B eserciterà una $\vec F_{B\rightarrow A}$ uguale e contraria sul corpo A
- le due forze hanno stessa direzione, modulo e verso opposto
- le due forze hanno la stessa retta d’azione (non sono solo parallele, ma sono collineari)
b) Quando un sistema si dice isolato?
Vedi qui.
c) Se considero un sistema che prevede delle forze di reazione, mi fanno escludere a priori che il sistema sia isolato, oppure non è vero? La legge vale sempre?
Possiamo considerare due casi:
- le forze di reazione sono tutte interne al sistema: non possiamo dire a priori se il sistema è isolato perché le forze interne si compensano sempre a coppie (per il terzo principio), ma per essere davvero isolato è necessario che anche le forze esterne siano nulle o si bilancino
- alcune o tutte le forze di reazione sono esterne al sistema: allora il sistema non è isolato perché perché c’è un interazione con l’esterno che può modificare la quantità di moto totale
La legge di azione e reazione non vale nei sistemi non inerziali in cui sono presenti forze apparenti causate da accelerazioni o rotazioni del sistema di riferimento.
Se pensiamo a una palla all’interno di una macchina, quando la macchina accelera la palla si muoverà in direzione opposta e all’interno dell’abitacolo la forza apparente che muove la palla non è contrastata da nessuna reazione, rompendo così la terza legge di Newton.