Lavoro ed Energia
Lavoro
Il lavoro viene definito quando si mette la forza in funzione della posizione occupata dal punto, in particolare il lavoro infinitesimo $dW$ compiuto dalla forza è definito come il prodotto scalare della forza per lo spostamento:
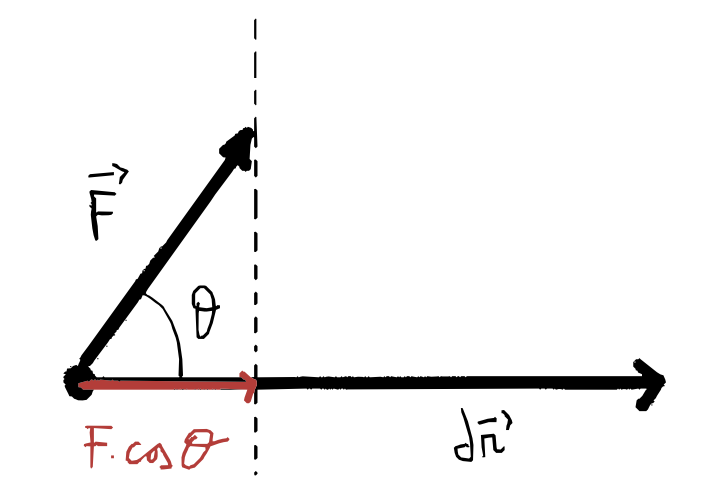
Con $\theta$ l’angolo formato da $\vec F$ e $d\vec r$:
- $\theta \in \big[0,\frac \pi 2\big[$ allora la proiezione della forza è concorde allo spostamento ed il lavoro è positivo
- $\theta = \frac \pi 2 \Rightarrow \cos \theta = 0$ e il lavoro diventa nullo
- $\theta > \frac \pi 2$ in questo caso la proiezione della forza è contraria allo spostamento ed il lavoro diventa negativo
Il lavoro è quella quantità che indica quanto una forza sta contribuendo allo spostamento, se:
- è positivo si dice lavoro motore
- è negativo si dice lavoro resistente
- altrimenti si dice lavoro nullo
Se si considera uno spostamento finito da A a B, dividendo la traiettoria in segmenti infinitesimi si può andare a calcolare il lavoro per ognuno di loro andando poi a sommarli insieme:
\[W_{tot} = \sum _{i=1}^N dW_i = \sum _{i=1}^N \vec F_i\cdot d\vec r_i\]
con $N\rightarrow \infty$
Il lavoro è definito come: \(W_{A\rightarrow B} = \int_A^B \vec F\cdot d\vec r\)
ovvero l’integrale di linea della forza lungo la traiettoria.
L’unità di misura del lavoro è il newton per metro che si chiama joule (pronuncia giul):
\[N\cdot m = kg \frac {m^2}{r^2} = J\]Energia cinetica
La definizione di lavoro é:
\[W_{i\rightarrow f} = \int_i^f \vec F\cdot d\vec r =\int_i^f F_T \cdot dr\]Facendo uso dell’equazione di Newton:
\[W_{i\rightarrow f} = \int_i^f m a_T \cdot d r = m\int_i^f \frac{d v }{dt} \cdot d r = m\int_i^f \frac{dr}{dt} dv = m\int_i^fvdv\] \[W_{i\rightarrow f} = \frac 12 mv_f^2 - \frac 12 mv_i^2 = E_{k,f} - E_{k,i}\]In cui la quantità $\frac 12 m v^2$ prende il nome di energia cinetica.
Il teorema dell’energia cinetica (teorema delle forze vive) afferma che:
il lavoro compiuto dalla risultante delle forza di un punto material da una posizione iniziale ad una posizione finale è uguale alla variazione di energia cinetica del punto materiale in quel tragitto
Forze conservative
Forza Peso
Applicando la definizione del lavoro per la forza peso:
\[W_{i\rightarrow f} = \int_i^f \vec F \cdot d\vec r = \vec F\cdot \int_i^f d\vec r = m\vec g\cdot(\vec r_f - \vec r_i)\]Ora scomponiamo nei suoi componenti $\Delta \vec r$
\[(\vec r_f - \vec r_i) = [(x_f -x_i)\hat x + (z_f -z_i)\hat z]\]ricordando che $\hat z \cdot \hat x = 0$ otteniamo:
\[W_{i\rightarrow f} = -mg\hat z\cdot [(x_f -x_i)\hat x + (z_f -z_i)\hat z] = -mg(z_f-z_i)\]
Si noti che $z_f - z_i <0$ quindi $W_{i\rightarrow f} > 0$
E’ importante notare che data la formula ottenuta:
\[W = -(mgz_i - mgz_i)\]il lavoro della forza peso non dipende dal percorso compiuto dalla massa, ma solamente dalla posizione iniziale e finale della massa
Forza elastica
Applicando la definizione del lavoro per la forza elastica:
\[W_{i\rightarrow f} = \int_i^f \vec F \cdot d\vec r = \int_i^f -kx\hat u_x \cdot d\vec x \hat u_x = -\bigg(\frac12 kx^2_f - \frac12 kx^2_i\bigg)\]Anche in questo caso il lavoro dipende solo dalla posizione iniziale e finale.
Forze conservative
Il lavoro della forza peso e della forza elastica dipende solamente dalla posizione iniziale e finale e non dal particolare percorso, quindi presi due percorsi che iniziano per $i$ e finiscono per $f$:
\[W = \int_i^f (\vec F_C \cdot d\vec r)_I = \int_i^f (\vec F_C \cdot d\vec r)_{II} = \int_i^f \vec F_C \cdot d\vec r\]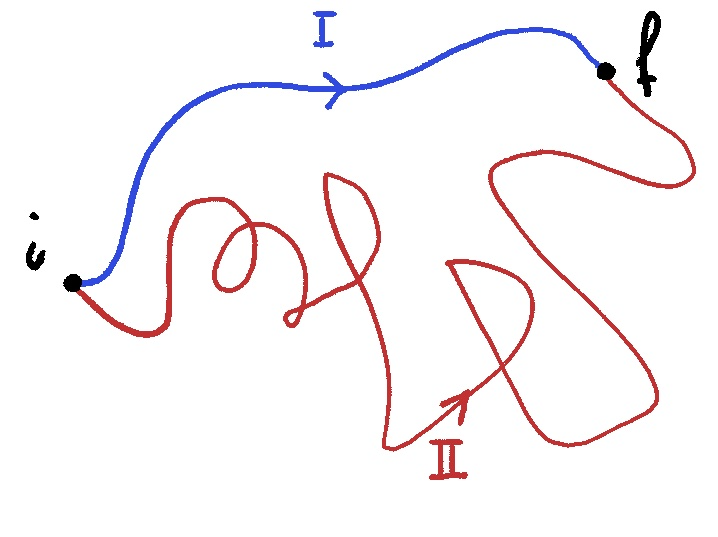
Invertendo il senso di percorrenza da $f$ a $i$, il lavoro compiuto è lo stesso in modulo, ma di segno opposto.
Un altra definizione per le forze conservative é che lungo un qualsiasi percorso chiuso il loro lavoro è nullo.
\[\oint \vec F d\vec s = 0\]Scegliando arbitrariamente due punti $i$ e $f$ all’interno del percorso chiuso:
\[\oint \vec F d\vec s = \int_i^f (\vec F d\vec s)_I + \int_f^i (\vec F d\vec s)_{II} = \int_i^f (\vec F d\vec s)_{I} - \int_i^f (\vec F d\vec s)_{II} = 0\] \[\Rightarrow \int_i^f (\vec F d\vec s)_{I} = \int_i^f (\vec F d\vec s)_{II}\]
Forze non conservative (attrito radente)
Il lavoro della forza di attrito radente è dato:
\[W = \int_i^f \vec F_a \cdot d\vec s = -\mu_d \int _i^f N\hat u_v\cdot d\vec s\]con $\hat u_v$ versore della velocità (la forza d’attrito è sempre contraria al moto del corpo) e nel caso la reazione vincolare $N$ sia costante:
\(W = -\mu_d N\int_i^f ds = -\mu_d Ns_{i\rightarrow f}\) Con $s_{i\rightarrow f}$ è la lunghezza del percorso, misurata lungo l’effettiva traiettoria del punto materiale.
Il lavoro della forza d’attrito radente dipende dal percorso e non è esprimibile tramite differenza dei valori di una funzione delle coordinate iniziali e finali.
Inoltre il lavoro della forza attrito è sempre negativo.
Energia potenziale
Il lavoro delle forze conservative dipende solo dalle posizioni iniziali e finali, quindi fissata una posizione di riferimento $O$ e considerando due posizioni $i$ e $f$:
\[W_{O\rightarrow O} = W_{Oi} + W_{if} + W_{fO} = 0\]Perché appunto un percorso chiuso e quindi possiamo ricavarci:
\[W_{if} = - W_{Oi} - W_{fO} = - W_{Oi} + W_{Of}\]Quindi definiamo come energia potenziale:
\[U_P = - W_{OP}\]Da cui possiamo quindi calcolare \(W_{i\rightarrow f} = - (U_f - U_i)\)
PROPRIETÀ:
- l’energia potenziale può essere definita solo per le forze conservative
- per tutte le forze conservative il lavoro si esprime come l’opposto della variazione di energia potenziale
- l’espressione per l’energia potenziale dipende dal tipo di forza e si ricava da \(U(\vec x_p) = - \int_O^P \vec F \cdot d\vec s\)
- l’energia potenziale è la primitiva della forza
Da notare che l’energia potenziale in un punto di per se non ha molto senso poiché dipende dalla scelta di $O$, ma ha senso parlare di differenza di energia potenziale che non dipende dalla scelta del riferimento.
Enerigia Meccanica e Teorema di conservazione dell’energia meccanica
Se agiscono solo forze conservative allora sono valide:
\[\begin{cases} W = E_{k, f} - E_{k, i} && \small\mathtt{Energia\;Cinetica}\\ \\ W = U(\vec x_i) - U(\vec x_f) && \small\mathtt{Energia\;Potenziale}\\ \end{cases}\]Eguagliando le due relazioni si ottiene:
\[E_{k, i} + U(\vec x_i) = E_{k, f} + U(\vec x_f)\]Tale somma si chiama energia meccanica e tale uguaglianza esprime il principio di conservazione dell’energia meccanica:
\[E_m = E_k + U = cost\]
- in un sistema isolato e in presenza di sole forze conservative l’energia meccanica di un punto materiale si conserva:
In generale non agiscono mai solo forze conservative, ma c’è sempre qualche forza non conservativa in gioco (attriti vari …) quindi l’energia meccanica non è mai costante.
In presenza di forze non conservative l’energia meccanica non resta costante e la sua variazione è uguale al lavoro delle forze non conservative:
\[W_{nc} = E_{m, i} - E_{m, f}\]
Domande
1) Parla della conservazione dell’energia meccanica.
Vedi l’energia meccanica.
2) Forze conservative. Esempi di forze conservative e non conservative.
3) Definisci energia potenziale (in generale)
Vedi l’energia potenziale.
4) Cosa sono le forze dissipative? Che ruolo hanno nel teorema generale della conservazione dell’energia meccanica?
Per forza dissipative si intendono le forze non conservative, quindi che il lavoro su un percorso chiuso non è nullo:
\[\oint \vec F_{nc}\cdot d\vec s \ne 0\]Queste forze trasformano una parte dell’energia meccanica in altri tipi di energia, tipicamente energia termica.
5) definizione di energia potenziale. Cos’è una forza conservativa. Esempi di forze conservative.
6) Si definisca il lavoro. Analisi dimensionale e senso fisico. Significato del prodotto scalare.
7) Ho una pallina che cade (in acqua? su un pavimento?) e dopo un po’ si ferma. Cosa è successo? Se volessimo scrivere un bilancio energetico?
- todo (va introdotto il caso dell’urto con il pavimento?)