vettori

Disegna le operazioni vettoriali che abbiamo studiato.

Prodotto tra un vettore ed uno scalare

Il prodotto di uno scalare $m$ (numero) per un vettore $\vec a$ ha come risultato un nuovo vettore avente stessa direzione di $\vec a$ e modulo $\lvert m \rvert$ volte quello di $\vec a$, lo stesso verso di $\vec a$ se $m > 0$, mentre verso opposto se $m<0$.

Grazie a questa operazione possiamo esprimere ogni vettore come il prodotto scalare del suo modulo per il vettore unitario $\hat u$ avente modulo 1 e direzione concorde ad $\hat a$. \(\vec a = a\cdot \hat u\)

Somma tra vettori

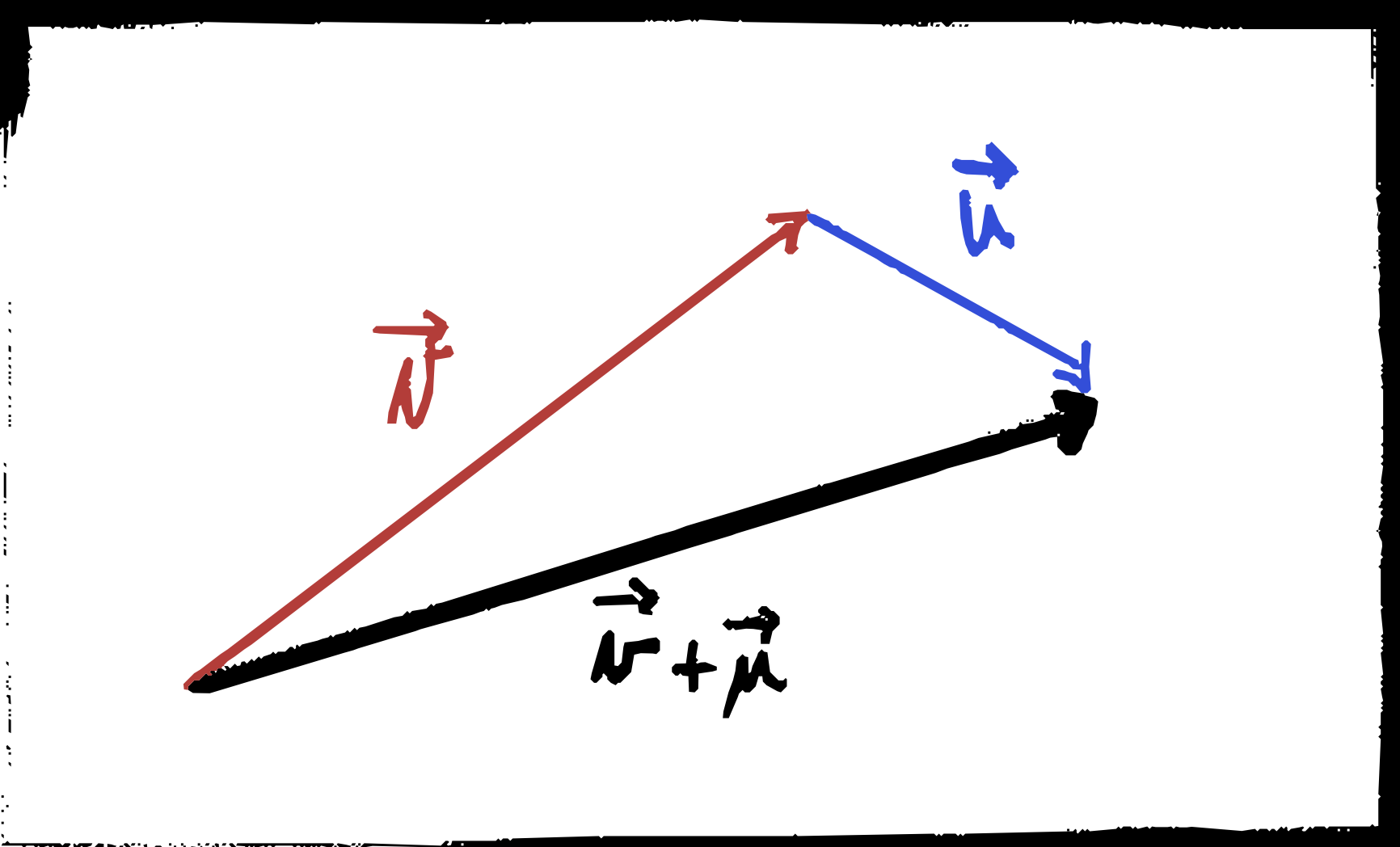
Dati due vettori $\vec a$ e $\vec b$ la loro somma è un vettore, detto vettore somma e indicato come \(\vec c = \vec a + \vec b\) Esso si ottiene graficamente disegnando il vettore $\vec b$ con punto di applicazione coincidente con il punto terminale di $\vec a$ e collegando il punto di applicazione di $\vec a$ con il punto terminale di $\vec b$.

Un’altra regola detta del parallelogramma: si disegnano il punto di applicazione di $\vec a$ e $\vec b$ coincidenti e $\vec c$ si ottiene disegnando la diagonale del parallelogramma con lati $\vec a$ e $\vec b$. Da quest’ultima regola si vede che la somma tra vettori è commutativa.

Si noti che con la somma si definisce implicitamente anche la differenza tra vettori, basti prendere l’opposto: \(\vec c = \vec a + (-\vec b)\) Nel caso di vettori paralleli si ha: \(\vec a_1 + \vec a_2 = a_1 \hat u + a_2 \hat u = (a_1 + a_2) \hat u\) Dato un sistema di riferimento è utile scomporre il vettore nelle sue componenti rispetto agli assi, quindi per esempio nel piano \(\vec a = a_x\cdot \hat u_x + a_y\cdot \hat u_y\)

Prodotto scalare

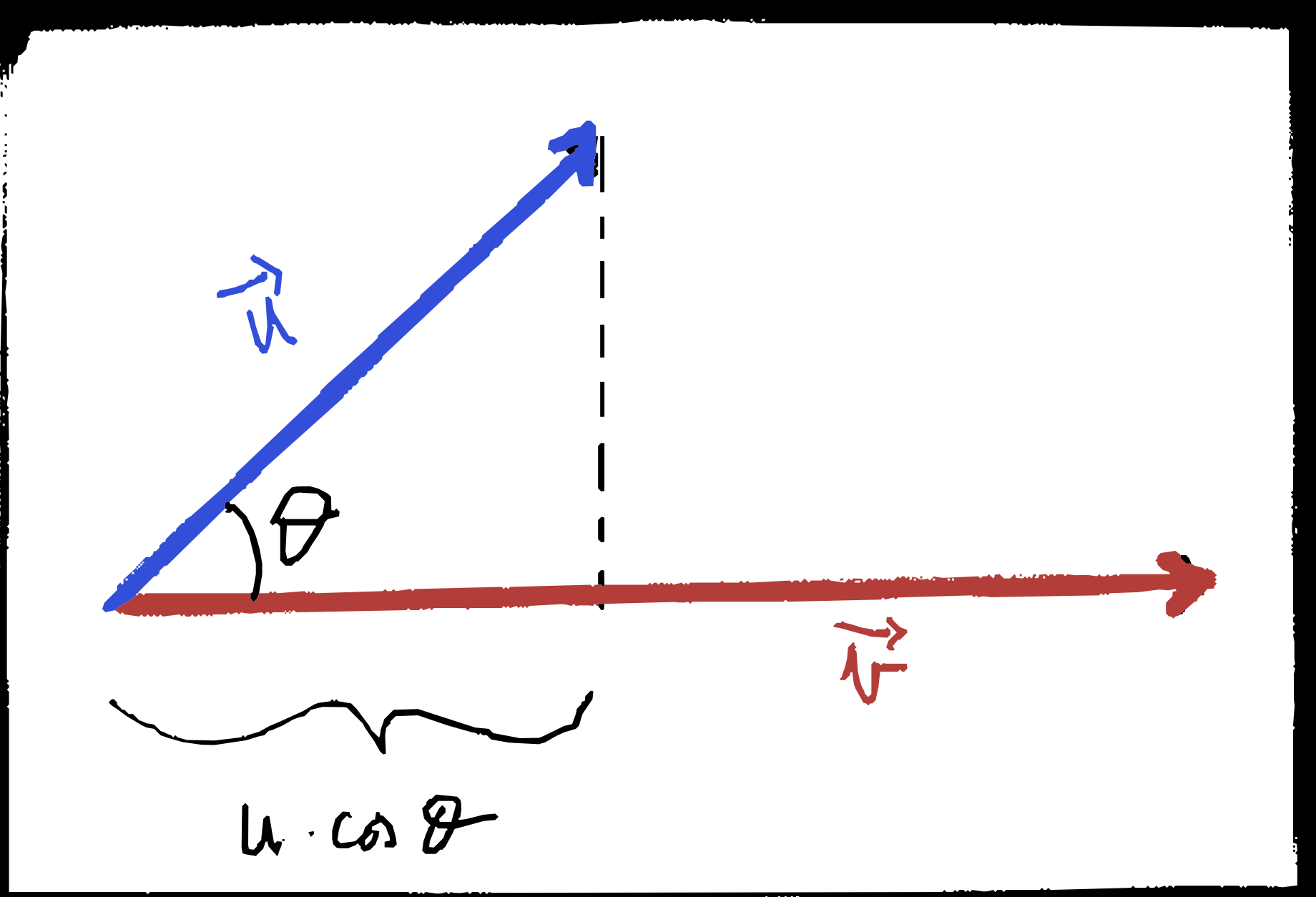
Dati due vettori $\vec a$ e $\vec b$ si definisce prodotto scalare la quantità \(s = \vec a \cdot \vec b = ||\vec a||\cdot ||\vec b|| \cdot \cos \theta\)

con $\theta$ l’angolo formato dai due vettori. Il risultato del prodotto scalare è uno scalare e gode delle seguenti:

1. il prodotto scalare è nullo solo se uno dei due vettori è nullo o se l’angolo compreso è $\frac\pi 2$
2. vale la proprietà commutativa \(\vec a \cdot \vec b = ||\vec a || \cdot || \vec b|| \cdot \cos (\theta) = ||\vec b || \cdot || \vec a|| \cdot \cos (-\theta) = \vec b \cdot \vec a\)
3. \(\vec a\cdot \vec a = || \vec a||\cdot || \vec a||\cdot \cos(0) = || \vec a||^2\)
4. vale la proprietà distributiva
5. non ha senso iterare il prodotto scalare: $\vec a \cdot \vec b \cdot \vec c$ è priva di senso perché appunto $\vec a \cdot \vec b$ è uno scalare e non può essere moltiplicato scalarmente per $\vec c$
6. se $\vec c = \vec a + \vec b$ dalla proprietà distributiva e dalla 3 allora \(||\vec c||^2 = (\vec a + \vec b)\cdot(\vec a + \vec b) = ||\vec a ||^2 + ||\vec b ||^2 + 2||\vec a||\, ||\vec b|| \cos \theta\) se $\vec a \perp \vec b$ allora \(c^2 = a^2 + b^2\) Fare il prodotto scalare tra due vettori scomposti negli assi ricordando che: \(\hat u_x \cdot \hat u_x = 1\quad \hat u_x \cdot \hat u_y = 0\) si ottiene che il prodotto scalare risulta uguale alla somma dei prodotti delle componenti omologhe sugli assi: \(\vec a \cdot \vec b = a_x b_x + a_y b_y\)

Infine un altro modo per visualizzare il prodotto scalare è quello di pensarlo come la moltiplicazione del modulo della proiezione di un vettore sul altro con il modulo del altro vettore.

Prodotto vettoriale

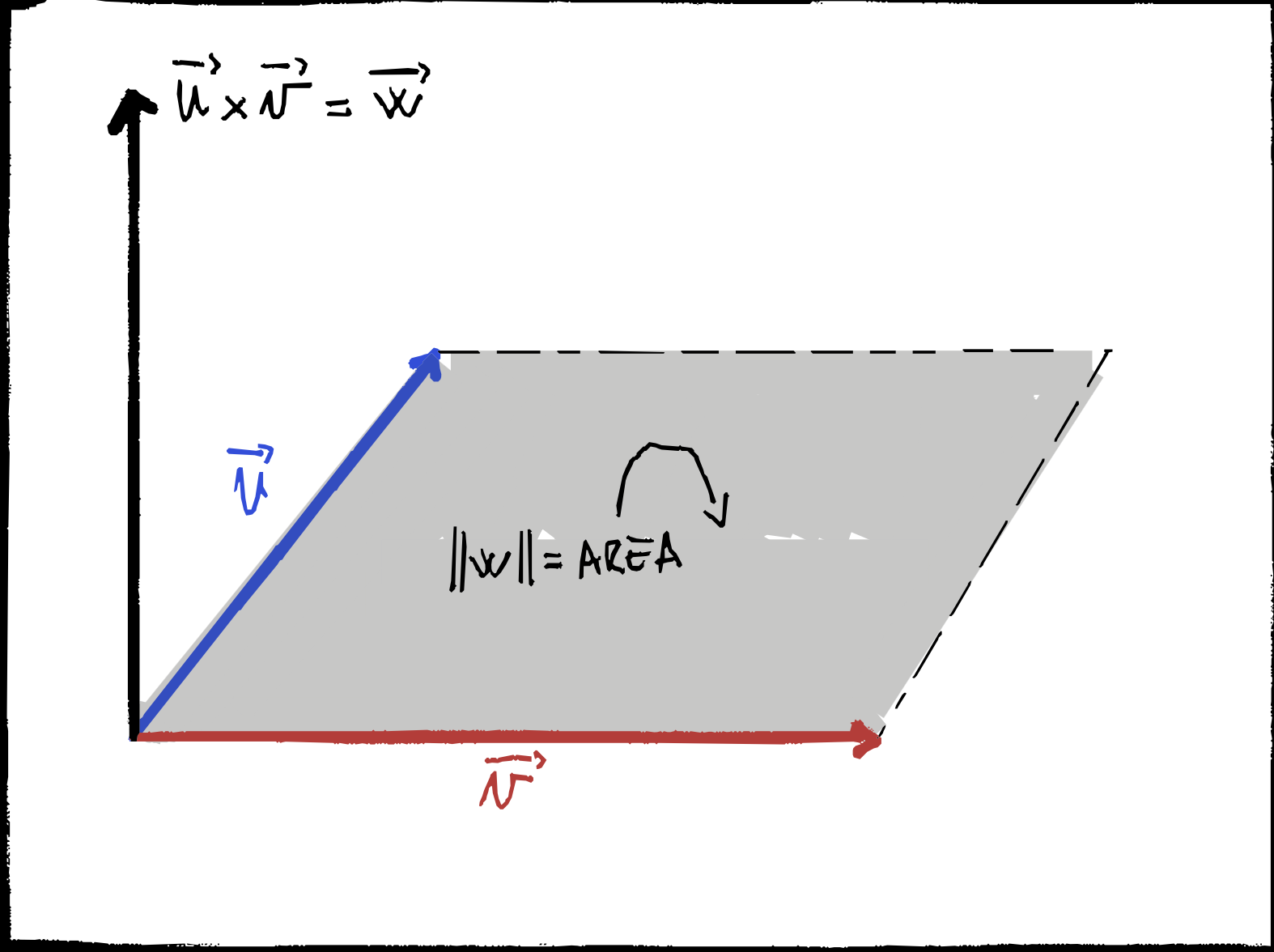
Il prodotto vettoriali di due vettori $\vec a$ e $\vec b$ risulta in un vettore $\vec c$ e si indica con \(\vec c = \vec a \times \vec b\) ed ha le seguenti caratteristiche:

1. la direzione è ortogonale al piano identificato da $\vec a$ e $\vec b$
2. il verso è definito dalla regola della regola della mano destra
3. il modulo $c = a \cdot b \cdot \sin \theta$ che corrisponde all’area del parallelogramma di lati a e b, di fatti $a\sin \theta$ corrisponde all’altezza del rettangolo con base b e viceversa. Il prodotto vettoriale è anticommutativo: \(\vec a \times \vec b = - \vec b \times \vec a\) Il prodotto vettoriale è nullo se uno dei due vettori è nullo o se i due vettori sono paralleli. Il prodotto vettoriale si può iterare, ma non è associativo quindi va specificato l’ordine.

todo

• derivata di un vettore
• integrale ???

Operazioni tra vettori. Prodotto vettoriale. Prodotto Scalare.

Vedi qui